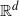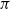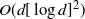Refine search
Actions for selected content:
149 results
Numerical method for solving impulse control problems in partially observed piecewise deterministic Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 15 December 2025, pp. 1-32
-
- Article
- Export citation
Diffusion approximation of the stationary distribution of a two-level single server queue
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1167-1205
- Print publication:
- December 2025
-
- Article
- Export citation
Some results on the supremum and on the first passage time of the generalized telegraph process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 453-491
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The impact of pinning points on memorylessness in Lévy random bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 15 October 2024, pp. 172-187
- Print publication:
- March 2025
-
- Article
- Export citation
Maintenance of steady-state mRNA levels by a microRNA-based feed forward loop in the presence of stochastic gene expression noise
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 29 May 2024, pp. 143-160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PDMP Monte Carlo methods for piecewise smooth densities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 1153-1194
- Print publication:
- December 2024
-
- Article
- Export citation
Tessellation-valued processes that are generated by cell division
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 01 November 2023, pp. 697-715
- Print publication:
- June 2024
-
- Article
- Export citation
Effects of concurrency on epidemic spreading in Markovian temporal networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 430-461
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adaptation of a population to a changing environment in the light of quasi-stationarity
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 235-286
- Print publication:
- March 2024
-
- Article
- Export citation
Chase–escape in dynamic device-to-device networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 311-339
- Print publication:
- March 2024
-
- Article
- Export citation
SIR epidemics driven by Feller processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 02 May 2023, pp. 1293-1316
- Print publication:
- December 2023
-
- Article
- Export citation
Moran models and Wright–Fisher diffusions with selection and mutation in a one-sided random environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 09 March 2023, pp. 701-767
- Print publication:
- September 2023
-
- Article
- Export citation
An ergodic theorem for asymptotically periodic time-inhomogeneous Markov processes, with application to quasi-stationarity with moving boundaries
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 672-700
- Print publication:
- June 2023
-
- Article
- Export citation
Convergence of blanket times for sequences of random walks on critical random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 09 January 2023, pp. 478-515
-
- Article
- Export citation
Exponential ergodicity for a class of Markov processes with interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 465-478
- Print publication:
- June 2023
-
- Article
- Export citation
Ruin probabilities in a Markovian shot-noise environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 542-556
- Print publication:
- June 2023
-
- Article
- Export citation
Matrix calculations for moments of Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 126-150
- Print publication:
- March 2023
-
- Article
- Export citation
A note on the polynomial ergodicity of the one-dimensional Zig-Zag process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 895-903
- Print publication:
- September 2022
-
- Article
- Export citation
Skew brownian motion and complexity of the alps algorithm
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 12 July 2022, pp. 777-796
- Print publication:
- September 2022
-
- Article
- Export citation
Unbiased filtering of a class of partially observed diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 661-687
- Print publication:
- September 2022
-
- Article
- Export citation