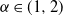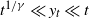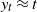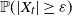Refine search
Actions for selected content:
59 results
Infinitely resizable urn models
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-35
-
- Article
- Export citation
Stable functional CLT for deterministic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3192-3222
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radially geometric stable distributions and processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. 1392-1429
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The impact of pinning points on memorylessness in Lévy random bridges
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 15 October 2024, pp. 172-187
- Print publication:
- March 2025
-
- Article
- Export citation
On the rate of convergence for an α-stable central limit theorem under sublinear expectation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 October 2024, pp. 209-233
- Print publication:
- March 2025
-
- Article
- Export citation
A remark on exact simulation of tempered stable Ornstein–Uhlenbeck processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1196-1198
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
Characteristics of the switch process and geometric divisibility
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 802-809
- Print publication:
- September 2024
-
- Article
- Export citation
Distribution of consensus in a broadcast-based consensus algorithm with random initial opinions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 09 May 2023, pp. 1416-1438
- Print publication:
- December 2023
-
- Article
- Export citation
Large deviations of Poisson Telecom processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 October 2022, pp. 267-283
- Print publication:
- March 2023
-
- Article
- Export citation
Non-asymptotic control of the cumulative distribution function of Lévy processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 913-944
- Print publication:
- September 2022
-
- Article
- Export citation
Exact simulation of Ornstein–Uhlenbeck tempered stable processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 347-371
- Print publication:
- June 2021
-
- Article
- Export citation
Tail asymptotics of an infinitely divisible space-time model with convolution equivalent Lévy measure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 25 February 2021, pp. 42-67
- Print publication:
- March 2021
-
- Article
- Export citation
SECOND ORDER SUBEXPONENTIALITY AND INFINITE DIVISIBILITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 22 June 2020, pp. 367-390
- Print publication:
- June 2022
-
- Article
- Export citation
Completely asymmetric stable processes conditioned to avoid an interval
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2019, pp. 1187-1197
- Print publication:
- December 2019
-
- Article
- Export citation
On perpetuities with gamma-like tails
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 2 / June 2018
- Published online by Cambridge University Press:
- 26 July 2018, pp. 368-389
- Print publication:
- June 2018
-
- Article
- Export citation
Random Fields with Pólya Correlation Structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1037-1050
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Nonnormal Small Jump Approximation of Infinitely Divisible Distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 963-984
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On a new Class of Tempered Stable Distributions: Moments and Regular Variation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1015-1035
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On Exact Sampling of Nonnegative Infinitely Divisible Random Variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 842-873
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
On a Class of Distributions Stable Under Random Summation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 303-318
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation