Refine search
Actions for selected content:
2 results
Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$
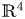
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1045-1070
- Print publication:
- June 2023
-
- Article
- Export citation
LEGENDRIAN GRAPHS GENERATED BY TANGENTIAL FAMILY GERMS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 02 February 2006, pp. 29-37
-
- Article
-
- You have access
- Export citation