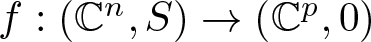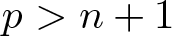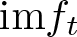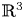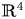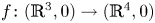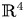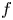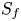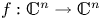Refine search
Actions for selected content:
8 results
Isotypical components of the homology of ICIS and images of deformations of map germs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-40
-
- Article
- Export citation
The dual tree of a fold map germ from $\mathbb {R}^{3}$
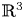 to $\mathbb {R}^{4}$
to $\mathbb {R}^{4}$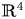
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 958-977
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
Kato–Matsumoto-type results for disentanglements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1-27
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
Bifurcation values of families of real curves
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1233-1242
- Print publication:
- December 2017
-
- Article
- Export citation
Projective dynamics of homogeneous systems: local invariants, syzygies and the Global Residue Theorem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 577-589
-
- Article
-
- You have access
- Export citation
Topological triviality of families of functions on analytic varieties
-
- Journal:
- Nagoya Mathematical Journal / Volume 175 / 2004
- Published online by Cambridge University Press:
- 22 January 2016, pp. 39-50
- Print publication:
- 2004
-
- Article
-
- You have access
- Export citation
On holomorphic maps with only fold singularities
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 147-184
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation