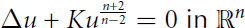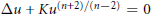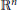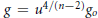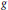Refine search
Actions for selected content:
4 results
The Fourth-Order Q-Curvature Flow on Closed 3-Manifolds
-
- Journal:
- Nagoya Mathematical Journal / Volume 185 / 2007
- Published online by Cambridge University Press:
- 11 January 2016, pp. 1-15
- Print publication:
- 2007
-
- Article
-
- You have access
- Export citation
The 2-Dimensional Calabi Flow
-
- Journal:
- Nagoya Mathematical Journal / Volume 181 / March 2006
- Published online by Cambridge University Press:
- 11 January 2016, pp. 63-73
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Global existence and convergence of solutions of the Calabi flow on Einstein 4-manifolds
-
- Journal:
- Nagoya Mathematical Journal / Volume 163 / September 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 193-214
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation
Growth Estimates on Positive Solutions of the Equation
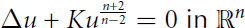
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 2 / 01 June 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 210-222
- Print publication:
- 01 June 2001
-
- Article
-
- You have access
- Export citation