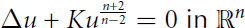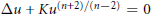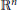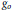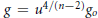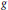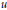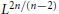Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Leung, Man Chun
2004.
Combining Solutions of Semilinear Partial Differential Equations in ℝnwith Critical Sobolev Exponent.
Communications in Partial Differential Equations,
Vol. 29,
Issue. 5-6,
p.
763.