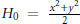Refine search
Actions for selected content:
4 results
Random dynamical systems with jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 890-910
- Print publication:
- September 2004
-
- Article
- Export citation
Une classe d’hamiltoniens polynomiaux isochrones
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 323-334
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation
The dynamic system method and the traps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 137-151
- Print publication:
- March 1998
-
- Article
- Export citation
Random perturbations of recursive sequences with an application to an epidemic model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 559-578
- Print publication:
- September 1995
-
- Article
- Export citation