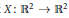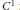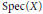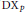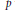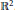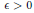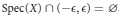Refine search
Actions for selected content:
3 results
On the Injectivity of C 1 Maps of the Real Plane
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 6 / 01 December 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1187-1201
- Print publication:
- 01 December 2002
-
- Article
-
- You have access
- Export citation
Non-expansive derived horseshoes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-415
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Diffeomorphisms with the shadowing property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 396-399
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation