Refine search
Actions for selected content:
3 results
DEFORMATIONS OF THE VERONESE EMBEDDING AND FINSLER
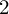 $2$-SPHERES OF CONSTANT CURVATURE
$2$-SPHERES OF CONSTANT CURVATURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 2103-2134
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
On holomorphic maps with only fold singularities
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 147-184
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
CR Mappings of Circular CR Manifolds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 4 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 396-407
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation