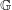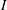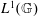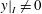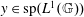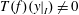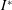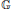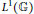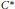Refine search
Actions for selected content:
4 results
Ideals of the Quantum Group Algebra, Arens Regularity and Weakly Compact Multipliers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 January 2020, pp. 825-836
- Print publication:
- December 2020
-
- Article
- Export citation
A Homological Property and Arens Regularity of Locally Compact Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 122-130
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
A residue formula for the fundamental Hochschild class on the Podleś sphere
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 257-271
- Print publication:
- October 2013
-
- Article
- Export citation
On Amenability and Co-Amenability of Algebraic Quantum Groups and Their Corepresentations
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 1 / 01 February 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-60
- Print publication:
- 01 February 2005
-
- Article
-
- You have access
- Export citation