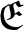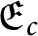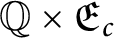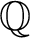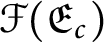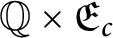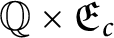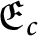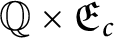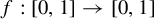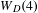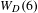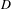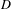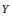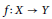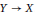Refine search
Actions for selected content:
6 results
A characterization of the product of the rational numbers and complete Erdős space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 87-102
- Print publication:
- March 2023
-
- Article
- Export citation
A characterization of a map whose inverse limit is an arc
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2533-2549
- Print publication:
- August 2022
-
- Article
- Export citation
ORBIFOLD POINTS ON PRYM–TEICHMÜLLER CURVES IN GENUS
 $4$
$4$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 May 2017, pp. 673-706
- Print publication:
- July 2019
-
- Article
- Export citation
Monotone Classes of Dendrites
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 3 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 675-697
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
A CRITERION FOR ERDŐS SPACES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 48 / Issue 3 / October 2005
- Published online by Cambridge University Press:
- 15 September 2005, pp. 595-601
-
- Article
-
- You have access
- Export citation
On Almost Continuous Mappings and Baire Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 21 / Issue 2 / 01 June 1978
- Published online by Cambridge University Press:
- 20 November 2018, pp. 183-186
- Print publication:
- 01 June 1978
-
- Article
-
- You have access
- Export citation