Refine search
Actions for selected content:
15 results
Cohomological and motivic inclusion–exclusion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2228-2283
- Print publication:
- September 2024
-
- Article
- Export citation
A DEDEKIND-STYLE AXIOMATIZATION AND THE CORRESPONDING UNIVERSAL PROPERTY OF AN ORDINAL NUMBER SYSTEM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 1396-1418
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MCKINSEY–TARSKI THEOREM FOR LOCALLY COMPACT ORDERED SPACES
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 187-211
- Print publication:
- June 2021
-
- Article
- Export citation
VARIETIES OF POSITIVE MODAL ALGEBRAS AND STRUCTURAL COMPLETENESS
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 13 June 2019, pp. 557-588
- Print publication:
- September 2019
-
- Article
- Export citation
On Countable Dense and n-homogeneity
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 4 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 860-869
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
Homogeneous Suslinian Continua
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 2 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 244-248
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON PARACOMPACT p-SPACES AND THE MONOTONE D-PROPERTY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 463-469
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
SOME CHARACTERIZATIONS OF COMMUTATIVE SUBSPACE LATTICES
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 02 February 2004, pp. 252-262
- Print publication:
- March 2004
-
- Article
- Export citation
The Nachibin quasi-uniformity of a bi-Stonian space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-326
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Separators in Continuous Images of Ordered Continua and Hereditarily Locally Connected Continua
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 2 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 154-163
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation
On Homogeneous Images of Compact Ordered Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 2 / 01 April 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 380-393
- Print publication:
- 01 April 1993
-
- Article
-
- You have access
- Export citation
Sandwich Theorems for Semicontinuous Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 4 / 01 December 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-474
- Print publication:
- 01 December 1992
-
- Article
-
- You have access
- Export citation
Connected Maps and Essentially Connected Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-194
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation
A Compactification for Convergence Ordered Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 505-513
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation
Partial Orders on the 2-Cell
-
- Journal:
- Canadian Mathematical Bulletin / Volume 18 / Issue 3 / August 1975
- Published online by Cambridge University Press:
- 20 November 2018, pp. 411-416
- Print publication:
- August 1975
-
- Article
-
- You have access
- Export citation
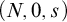
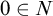
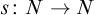
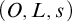
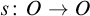

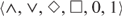

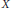
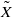 be the minimal dense linearly ordered extension of
be the minimal dense linearly ordered extension of 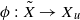 , ϕ(〈
, ϕ(〈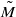 is a paracompact
is a paracompact 