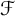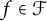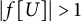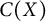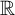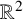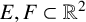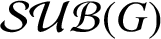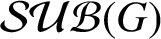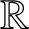Refine search
Actions for selected content:
12 results
Nowhere constant families of maps and resolvability
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 February 2024, pp. 701-705
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ARITHMETIC SUMS OF CONNECTED SETS IN
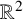 $\mathbb {R}^2$
$\mathbb {R}^2$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 507-519
- Print publication:
- June 2023
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation
GEOGRAPHY AND BOTANY OF IRREDUCIBLE NON-SPIN SYMPLECTIC 4-MANIFOLDS WITH ABELIAN FUNDAMENTAL GROUP
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 13 August 2013, pp. 261-281
- Print publication:
- May 2014
-
- Article
-
- You have access
- Export citation
First Countable Continua and Proper Forcing
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 3 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 604-616
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
Characterizing Continua by Disconnection Properties
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 3 / 01 September 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 348-358
- Print publication:
- 01 September 1998
-
- Article
-
- You have access
- Export citation
Every Countable Regular Space Without Isolated Points is Connectifiable
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 4 / 01 December 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 556-559
- Print publication:
- 01 December 1994
-
- Article
-
- You have access
- Export citation
A Topological Banach Fixed Point Theorem for Compact Hausdorff Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 4 / 01 December 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 552-555
- Print publication:
- 01 December 1994
-
- Article
-
- You have access
- Export citation
Local Connectedness of the stone-Čech Compactification
-
- Journal:
- Canadian Mathematical Bulletin / Volume 31 / Issue 2 / 01 June 1988
- Published online by Cambridge University Press:
- 20 November 2018, pp. 236-240
- Print publication:
- 01 June 1988
-
- Article
-
- You have access
- Export citation
Connectedness Properties of Lattices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 29 / Issue 3 / 01 September 1986
- Published online by Cambridge University Press:
- 20 November 2018, pp. 314-320
- Print publication:
- 01 September 1986
-
- Article
-
- You have access
- Export citation
Connected Maps and Essentially Connected Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 190-194
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation
On almost locally connected spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-264
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation