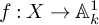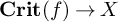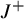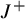Refine search
Actions for selected content:
7 results
A DERIVED LAGRANGIAN FIBRATION ON THE DERIVED CRITICAL LOCUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 31 August 2022, pp. 311-345
- Print publication:
- January 2024
-
- Article
- Export citation
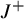 $J^+$-invariants for planar two-center Stark–Zeeman systems
$J^+$-invariants for planar two-center Stark–Zeeman systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 24 May 2022, pp. 2258-2292
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost existence from the feral perspective and some questions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 792-834
- Print publication:
- February 2022
-
- Article
- Export citation
A HYDRODYNAMICAL HOMOTOPY CO-MOMENTUM MAP AND A MULTISYMPLECTIC INTERPRETATION OF HIGHER-ORDER LINKING NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 11 February 2021, pp. 335-354
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
BEREZIN–TOEPLITZ QUANTIZATION, HYPERKÄHLER MANIFOLDS, AND MULTISYMPLECTIC MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 167-187
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
On symplectic fillings of links of rational surface singularities with reduced fundamental cycle
-
- Journal:
- Nagoya Mathematical Journal / Volume 175 / 2004
- Published online by Cambridge University Press:
- 22 January 2016, pp. 51-57
- Print publication:
- 2004
-
- Article
-
- You have access
- Export citation
Finite Groups Generated by Involutions on Lagrangian Planes of C 2
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 4 / 01 December 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 408-419
- Print publication:
- 01 December 2001
-
- Article
-
- You have access
- Export citation