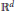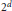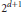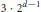Refine search
Actions for selected content:
5 results
A NOTE ON MARKOVIAN QUANTUM DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 436-445
-
- Article
-
- You have access
- Export citation
On the X-ray Number of Almost Smooth Convex Bodies and of Convex Bodies of Constant Width
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 3 / 01 September 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 342-348
- Print publication:
- 01 September 2009
-
- Article
-
- You have access
- Export citation
On the Bezdek–Pach Conjecture for Centrally Symmetric Convex Bodies
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 3 / 01 September 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 407-415
- Print publication:
- 01 September 2009
-
- Article
-
- You have access
- Export citation
Independence for Sets of Topological Spheres
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 4 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 520-524
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation
Continuous Families of Smooth Curves and Grünbaum’s Conjecture
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 3 / 01 September 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 345-350
- Print publication:
- 01 September 1984
-
- Article
-
- You have access
- Export citation