Refine search
Actions for selected content:
7 results
Approximations of positive operators and continuity of the spectral radius III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-340
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Existence of Invariant Weak Units in Banach Lattices: Countably Generated Left Amenable Semigroup of Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 6 / 01 December 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1299-1312
- Print publication:
- 01 December 1993
-
- Article
-
- You have access
- Export citation
Some Characterizations of Dedekind α-Completeness of a Riesz Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 1 / 01 March 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-7
- Print publication:
- 01 March 1993
-
- Article
-
- You have access
- Export citation
Representation of p-Lattice Summing Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 2 / 01 June 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-277
- Print publication:
- 01 June 1992
-
- Article
-
- You have access
- Export citation
A Mean Ergodic Theorem for Multiparameter Superadditive Processes on Banach Lattices
-
- Journal:
- Canadian Journal of Mathematics / Volume 42 / Issue 6 / 01 December 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1018-1040
- Print publication:
- 01 December 1990
-
- Article
-
- You have access
- Export citation
Interpolation and Spectra of Regular LP -Space Operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 4 / 01 December 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 470-481
- Print publication:
- 01 December 1990
-
- Article
-
- You have access
- Export citation
Lattice Dilations of Positive Contractions on L p-Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 3 / 01 September 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-374
- Print publication:
- 01 September 1982
-
- Article
-
- You have access
- Export citation
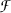 ,
, 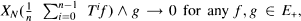 where
where 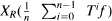 converges in norm.
converges in norm.