Refine search
Actions for selected content:
35 results
Quantitative ergodic theorems for actions of groups of polynomial growth
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 04 September 2025, pp. 128-181
- Print publication:
- January 2026
-
- Article
- Export citation
A Kakutani–Rokhlin decomposition for conditionally ergodic process in the measure-free setting of vector lattices
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 05 August 2025, pp. 3600-3618
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASI-ERGODICITY OF COMPACT STRONG FELLER SEMIGROUPS ON
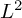 $L^2$
$L^2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 541-584
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the speed of convergence in the ergodic theorem for shift operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 04 November 2024, pp. 1919-1937
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pure point spectrum for dynamical systems and mean, Besicovitch and Weyl almost periodicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 524-568
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness and stability of equilibrium states for random non-uniformly expanding maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 27 July 2022, pp. 2589-2623
- Print publication:
- August 2023
-
- Article
- Export citation
SPECTRAL CONDITIONS FOR UNIFORM P-ERGODICITIES OF MARKOV OPERATORS ON ABSTRACT STATES SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 23 September 2020, pp. 682-696
- Print publication:
- September 2021
-
- Article
- Export citation
Note on Spectra of Non-Selfadjoint Operators Over Dynamical Systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 371-386
-
- Article
- Export citation
THE CESÀRO OPERATOR IN THE FRÉCHET SPACES ℓp+ AND L p−
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 273-287
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
Computing Solutions of the Yang-Baxter-like Matrix Equation for Diagonalisable Matrices
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 5 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 75-84
- Print publication:
- February 2015
-
- Article
- Export citation
Random dynamical systems with jumps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 890-910
- Print publication:
- September 2004
-
- Article
- Export citation
Countable Amenable Identity Excluding Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 2 / 01 June 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 215-228
- Print publication:
- 01 June 2004
-
- Article
-
- You have access
- Export citation
A Larger Class of Ornstein Transformations with Mixing Property
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 2 / 01 June 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-161
- Print publication:
- 01 June 2000
-
- Article
-
- You have access
- Export citation
Spectral and asymptotic properties of dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-31
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
A Family of Generalized Riesz Products
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 2 / 01 April 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 302-315
- Print publication:
- 01 April 1996
-
- Article
-
- You have access
- Export citation
Moving Ergodic Theorems for Superadditive Processes
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 4 / 01 August 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 728-743
- Print publication:
- 01 August 1995
-
- Article
-
- You have access
- Export citation
The Group of Eigenvalues of a Rank One Transformation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 1 / 01 March 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 42-54
- Print publication:
- 01 March 1995
-
- Article
-
- You have access
- Export citation
The Maximal Spectral Type of a Rank One Transformation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-36
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
Moving Weighted Averages
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 3 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-469
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation
A Multiparameter, Zero Density Subsequence Ergodic Theorem
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 1 / 01 March 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-37
- Print publication:
- 01 March 1993
-
- Article
-
- You have access
- Export citation
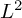








 . We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.
. We discuss several applications and illustrate our results with examples. This includes a complete description of quasi-ergodicity for a large class of semigroups corresponding to non-local Schrödinger operators with confining potentials.


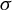
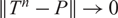
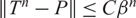
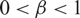
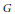
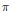
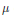
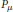
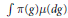
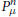
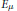
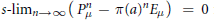
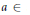
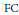
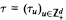 be a semigroup of measure preserving transformations on a measure space (Ω, ℱ, μ). The main result of the paper is the proof of a.e. convergence for the moving averages
be a semigroup of measure preserving transformations on a measure space (Ω, ℱ, μ). The main result of the paper is the proof of a.e. convergence for the moving averages 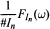
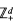 satisfying the "cone-condition". The identification of the limit is given. A moving local theorem is also proved.
satisfying the "cone-condition". The identification of the limit is given. A moving local theorem is also proved.