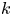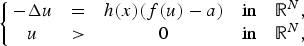Refine search
Actions for selected content:
6 results
SUMMABILITY AND ASYMPTOTICS OF POSITIVE SOLUTIONS OF AN EQUATION OF WOLFF TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 535-544
- Print publication:
- December 2024
-
- Article
- Export citation
Propagation of minima for nonlocal operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 23 May 2023, pp. 1033-1046
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of positive solutions for a class of semipositone problem in whole ℝN
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 05 April 2019, pp. 2349-2367
- Print publication:
- October 2020
-
- Article
- Export citation
Lotka–Volterra models with fractional diffusion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 505-528
- Print publication:
- June 2017
-
- Article
- Export citation
Linear non-local diffusion problems in metric measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 833-863
- Print publication:
- August 2016
-
- Article
- Export citation
NONLINEAR VOLTERRA INTEGRAL EQUATIONS WITH CONVOLUTION KERNELS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 4 / July 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 484-490
- Print publication:
- July 2003
-
- Article
- Export citation