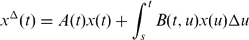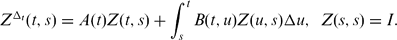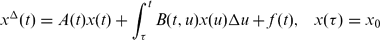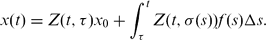Refine search
Actions for selected content:
11 results
Continuum limit for interacting systems on adaptive networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 December 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discounted probability of exponential parisian ruin: Diffusion approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 17-37
- Print publication:
- March 2022
-
- Article
- Export citation
Mass-conserving solutions to the Smoluchowski coagulation equation with singular kernel
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 19 February 2019, pp. 1805-1825
- Print publication:
- August 2020
-
- Article
- Export citation
Globally Asymptotic Stability of a Delayed Integro-Differential Equation With Nonlocal Diffusion
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 436-448
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
Periodic Solutions of Almost Linear Volterra Integro-dynamic Equations on Periodic Time Scales
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-181
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
Convergence Analysis of Legendre-Collocation Methods for Nonlinear Volterra Type Integro Equations
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 09 January 2015, pp. 74-88
- Print publication:
- February 2015
-
- Article
- Export citation
A Spectral Method for Neutral Volterra Integro-Differential Equation with Weakly Singular Kernel
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 424-446
- Print publication:
- May 2013
-
- Article
- Export citation
Three Fixed Point Theorems: Periodic Solutions of a Volterra Type Integral Equation with Infinite Heredity
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-91
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
Convergence Analysis of the Spectral Methods for Weakly Singular Volterra Integro-Differential Equations with Smooth Solutions
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 4 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1-20
- Print publication:
- February 2012
-
- Article
- Export citation
PRINCIPAL MATRIX SOLUTIONS AND VARIATION OF PARAMETERS FOR VOLTERRA INTEGRO-DYNAMIC EQUATIONS ON TIME SCALES
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 10 March 2011, pp. 463-480
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Smooth Values of the Iterates of the Euler Phi-Function
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 1 / 01 February 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 127-147
- Print publication:
- 01 February 2007
-
- Article
-
- You have access
- Export citation