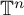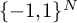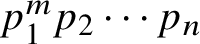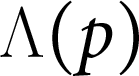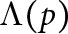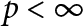Refine search
Actions for selected content:
14 results
Arens regularity of ideals of the group algebra of a compact Abelian group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 718-734
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VARIANTS OF A MULTIPLIER THEOREM OF KISLYAKOV
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 September 2022, pp. 347-377
- Print publication:
- January 2024
-
- Article
- Export citation
Extreme cases for Frostman’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 August 2022, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Amenability, proximality and higher-order syndeticity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 May 2022, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Non-abelian, Non-Sidon, Completely Bounded
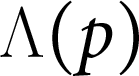 $\Lambda (p)$ Set
$\Lambda (p)$ Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 1-7
- Print publication:
- March 2021
-
- Article
- Export citation
Sidon Sets are Proportionally Sidon with Small Sidon Constants
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 798-809
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
The Relationship Between ϵ-Kronecker Sets and Sidon Sets
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 3 / 01 September 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 521-527
- Print publication:
- 01 September 2016
-
- Article
-
- You have access
- Export citation
Transfer of Fourier Multipliers into Schur Multipliers and Sumsets in a Discrete Group
-
- Journal:
- Canadian Journal of Mathematics / Volume 63 / Issue 5 / 18 October 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1161-1187
- Print publication:
- 18 October 2011
-
- Article
-
- You have access
- Export citation
CYCLES AND 1-UNCONDITIONAL MATRICES
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 93 / Issue 3 / November 2006
- Published online by Cambridge University Press:
- 13 October 2006, pp. 761-790
- Print publication:
- November 2006
-
- Article
- Export citation
HYPONORMAL OPERATORS, WEIGHTED SHIFTS AND WEAK FORMS OF SUPERCYCLICITY
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 49 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 02 February 2006, pp. 1-15
-
- Article
-
- You have access
- Export citation
Maximal Operators and Cantor Sets
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 330-342
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
U-Sets in Compact, 0-Dimensional, Metric Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 2 / 01 June 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-155
- Print publication:
- 01 June 1989
-
- Article
-
- You have access
- Export citation
Finite Unions of Quasi-Independent Sets
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 490-493
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation