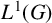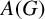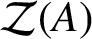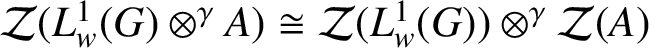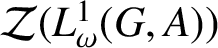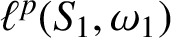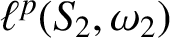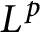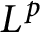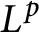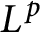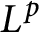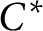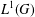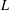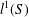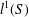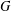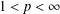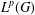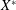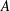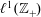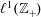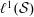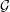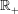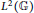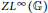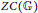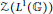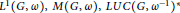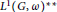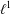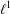Refine search
Actions for selected content:
46 results
Weak amenability for dual Banach algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 740-748
-
- Article
- Export citation
On the Dales–Żelazko conjecture for Beurling algebras on discrete groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 613-624
-
- Article
- Export citation
A CRITERION FOR HYPERSYMMETRY ON DISCRETE GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 05 December 2022, pp. 320-330
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLIERS ON THE SECOND DUAL OF ABSTRACT SEGAL ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 133-141
- Print publication:
- August 2023
-
- Article
- Export citation
CENTRE OF BANACH ALGEBRA VALUED BEURLING ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 490-498
- Print publication:
- June 2022
-
- Article
- Export citation
Uniformly quasi-Hermitian groups are supramenable
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 July 2021, pp. 665-673
- Print publication:
- September 2022
-
- Article
- Export citation
ON ALGEBRA ISOMORPHISMS BETWEEN p-BANACH BEURLING ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 11 January 2021, pp. 308-319
- Print publication:
- October 2021
-
- Article
- Export citation
On isomorphisms between weighted
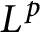 $L^p$-algebras
$L^p$-algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 853-866
- Print publication:
- December 2021
-
- Article
- Export citation
Ring-theoretic (In)finiteness in reduced products of Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1423-1458
- Print publication:
- October 2021
-
- Article
- Export citation
ZERO JORDAN PRODUCT DETERMINED BANACH ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2020, pp. 145-158
- Print publication:
- October 2021
-
- Article
- Export citation
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
THE FIRST COHOMOLOGY GROUP OF BANACH INVERSE SEMIGROUP ALGEBRAS WITH COEFFICIENTS IN
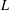 $L$-EMBEDDED BANACH BIMODULES
$L$-EMBEDDED BANACH BIMODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 September 2019, pp. 488-495
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
HYPERREFLEXIVITY CONSTANTS OF THE BOUNDED
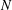 $N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS
$N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 112-130
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Fourier Spaces and Completely Isometric Representations of Arens Product Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 717-747
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Simplicial (Co)-homology of
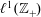 $\ell ^{1}(\mathbb{Z}_{+})$
$\ell ^{1}(\mathbb{Z}_{+})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 756-766
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Character Density in Central Subalgebras of Compact Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-461
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
New Deformations of Convolution Algebras and Fourier Algebras on Locally Compact Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 2 / 01 April 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-452
- Print publication:
- 01 April 2017
-
- Article
-
- You have access
- Export citation
Bipositive Isomorphisms Between Beurling Algebras and Between their Second Dual Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-20
- Print publication:
- 01 February 2017
-
- Article
-
- You have access
- Export citation
COMPACT ELEMENTS AND OPERATORS OF QUANTUM GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 445-462
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
HOMOMORPHISMS OF
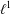 $\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
$\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 115-122
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation