Refine search
Actions for selected content:
5 results
An endpoint estimate for product singular integral operators on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Marcinkiewicz Multipliers and Lipschitz Spaces on Heisenberg Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 607-627
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A Dimension-Free Weak-Type Estimate for Operators on UMD-Valued Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 43 / Issue 3 / 01 September 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 355-361
- Print publication:
- 01 September 2000
-
- Article
-
- You have access
- Export citation
S and g*λ-functions on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-344
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Exponential Estimates for the Conjugate Function on Locally Compact Abelian Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 1 / 01 March 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 34-44
- Print publication:
- 01 March 1990
-
- Article
-
- You have access
- Export citation
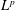
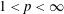
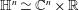
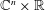
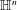
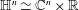
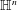
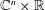
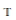
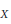
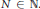
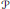
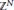
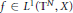
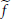
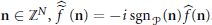
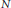
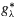 -functions.
-functions.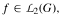 the conjugate function of
the conjugate function of 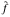 whose Fourier transform satisfies the identity
whose Fourier transform satisfies the identity 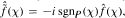 for almost all
for almost all 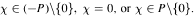 We prove that, when
We prove that, when 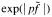 is integrable for all
is integrable for all 