Refine search
Actions for selected content:
12 results
Karamata’s theorem for regularized Cauchy transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1431-1491
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FIXED POINT THEOREM FOR AN INFINITE TOEPLITZ MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 108-117
- Print publication:
- August 2021
-
- Article
- Export citation
TAUBERIAN THEOREMS AND SPECTRAL THEORY IN TOPOLOGICAL VECTOR SPACES
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 511-532
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Asymptotic analysis for personalized Web search
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 577-604
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Optimal Control of a Large Dam
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 249-258
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Weighted Convolution Operators on ℓp
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 2 / 01 June 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 175-179
- Print publication:
- 01 June 2005
-
- Article
-
- You have access
- Export citation
Inverse Problems for Partition Functions
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 4 / 01 August 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 866-896
- Print publication:
- 01 August 2001
-
- Article
-
- You have access
- Export citation
Generalized regular variation of second order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 381-395
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
Tauberian- and Convexity Theorems for Certain (N,p,q)-Means
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 5 / 01 October 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 982-994
- Print publication:
- 01 October 1994
-
- Article
-
- You have access
- Export citation
New Tauberian Theorems from Old
-
- Journal:
- Canadian Journal of Mathematics / Volume 46 / Issue 2 / 01 April 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 380-394
- Print publication:
- 01 April 1994
-
- Article
-
- You have access
- Export citation
A Karamata Method I. Elementary Properties and Applications
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 2 / 01 June 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 147-157
- Print publication:
- 01 June 1991
-
- Article
-
- You have access
- Export citation
Abel Transformations Into I 1
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 4 / 01 December 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 421-427
- Print publication:
- 01 December 1982
-
- Article
-
- You have access
- Export citation
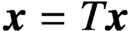
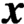
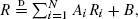 where the
where the 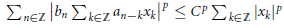
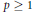
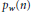
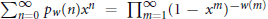
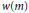
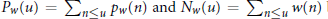
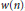
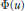
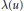
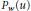
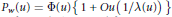
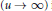
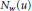
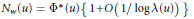
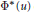
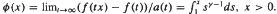 . Then
. Then 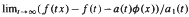 exists non-trivially with a second auxiliary function a
exists non-trivially with a second auxiliary function a