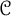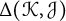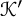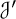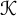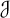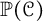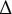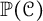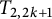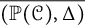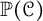We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use the cobordism distance on the smooth knot concordance group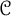 
$\mathcal {C}$ to measure how close two knots are to being linearly dependent. Our measure, 
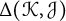$\Delta (\mathcal {K}, \mathcal {J})$, is built by minimizing the cobordism distance between all pairs of knots, 
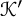$\mathcal {K}'$ and 
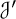$\mathcal {J}'$, in cyclic subgroups containing 
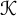$\mathcal {K}$ and 
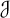$\mathcal {J}$. When made precise, this leads to the definition of the projective space of the concordance group, 
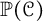${\mathbb P}(\mathcal {C})$, upon which 
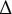$\Delta $ defines an integer-valued metric. We explore basic properties of 
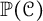${\mathbb P}(\mathcal {C})$ by using torus knots 
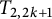$T_{2,2k+1}$. Twist knots are used to demonstrate that the natural simplicial complex 
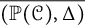$\overline {({\mathbb P}(\mathcal {C}), \Delta )}$ associated with the metric space 
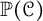${\mathbb P}(\mathcal {C})$ is infinite-dimensional.
