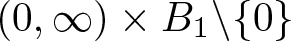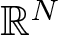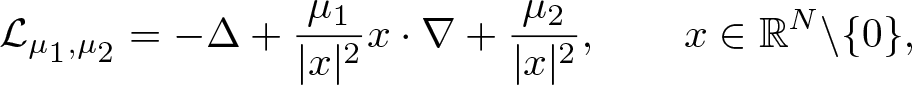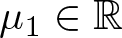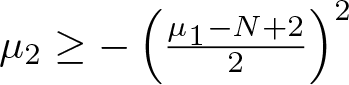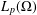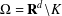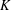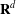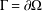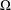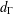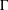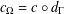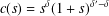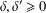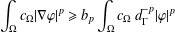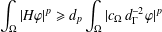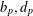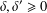In this paper, we establish suitable characterisations for a pair of functions  $(W(x),H(x))$ on a bounded, connected domain
$(W(x),H(x))$ on a bounded, connected domain  $\Omega \subset \mathbb{R}^n$ in order to have the following Hardy inequality:
$\Omega \subset \mathbb{R}^n$ in order to have the following Hardy inequality: \begin{equation*}\int_{\Omega} W(x) |\nabla u|_A^2 dx \geq \int_{\Omega} |\nabla d|^2_AH(x)|u|^2 dx, \,\,\, u \in C^{1}_0(\Omega),\end{equation*}
\begin{equation*}\int_{\Omega} W(x) |\nabla u|_A^2 dx \geq \int_{\Omega} |\nabla d|^2_AH(x)|u|^2 dx, \,\,\, u \in C^{1}_0(\Omega),\end{equation*}
where d(x) is a suitable quasi-norm (gauge),  $|\xi|^2_A = \langle A(x)\xi, \xi \rangle$ for
$|\xi|^2_A = \langle A(x)\xi, \xi \rangle$ for  $\xi \in \mathbb{R}^n$ and A(x) is an n × n symmetric, uniformly positive definite matrix defined on a bounded domain
$\xi \in \mathbb{R}^n$ and A(x) is an n × n symmetric, uniformly positive definite matrix defined on a bounded domain  $\Omega \subset \mathbb{R}^n$. We also give its Lp analogue. As a consequence, we present examples for a standard Laplacian on
$\Omega \subset \mathbb{R}^n$. We also give its Lp analogue. As a consequence, we present examples for a standard Laplacian on  $\mathbb{R}^n$, Baouendi–Grushin operator, and sub-Laplacians on the Heisenberg group, the Engel group and the Cartan group. Those kind of characterisations for a pair of functions
$\mathbb{R}^n$, Baouendi–Grushin operator, and sub-Laplacians on the Heisenberg group, the Engel group and the Cartan group. Those kind of characterisations for a pair of functions  $(W(x),H(x))$ are obtained also for the Rellich inequality. These results answer the open problems of Ghoussoub-Moradifam [16].
$(W(x),H(x))$ are obtained also for the Rellich inequality. These results answer the open problems of Ghoussoub-Moradifam [16].