Refine search
Actions for selected content:
8 results
Dependence Analysis of the Solutions on the Parameters of Fractional Neutral Delay Differential Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 772-783
- Print publication:
- October 2016
-
- Article
- Export citation
Existence of Solutions for Abstract Non-Autonomous Neutral Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 736-751
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
Stability Analysis of Runge-Kutta Methods for Nonlinear Neutral Volterra Delay-Integro-Differential Equations
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 4 / Issue 4 / November 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 537-561
- Print publication:
- November 2011
-
- Article
- Export citation
EXISTENCE OF S-ASYMPTOTICALLY ω-PERIODIC SOLUTIONS FOR ABSTRACT NEUTRAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 365-382
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Comparison Theorems of Liapunov-Razumikhin Type for NFDEs With Infinite Delay
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 3 / 01 June 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 500-526
- Print publication:
- 01 June 1995
-
- Article
-
- You have access
- Export citation
An Oscillation Result for Singular Neutral Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-65
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
Some Asymptotic Properties of Solutions of a Neutral Delay Equation With an Oscillatory Coefficient
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 3 / 01 September 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 263-272
- Print publication:
- 01 September 1993
-
- Article
-
- You have access
- Export citation
Hopf Bifurcation for Implicit Neutral Functional Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 3 / 01 September 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 286-295
- Print publication:
- 01 September 1993
-
- Article
-
- You have access
- Export citation
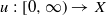 is said to be
is said to be 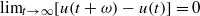 . This paper is devoted to study the existence and qualitative properties of
. This paper is devoted to study the existence and qualitative properties of