Refine search
Actions for selected content:
14 results
Optimal stopping zero-sum games in continuous hidden Markov models
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence and properties of semi-bounded global solutions to the functional differential equation with Volterra-type operators on the real line
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1119-1168
- Print publication:
- December 2017
-
- Article
- Export citation
Fitted Mesh Method for a Class of Singularly PerturbedDifferential-Difference Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 496-514
- Print publication:
- November 2015
-
- Article
- Export citation
Optimal Stopping Problems in Diffusion-Type Models with Running Maxima and Drawdowns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 799-817
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Bayesian Quickest Detection Problems for Some Diffusion Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 164-185
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Population dynamics with age-dependent diffusion and death rates
-
- Journal:
- European Journal of Applied Mathematics / Volume 24 / Issue 4 / August 2013
- Published online by Cambridge University Press:
- 21 February 2013, pp. 471-500
-
- Article
- Export citation
Fluxon Centering in Josephson Junctions with Exponentially Varying Width
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 2 / Issue 3 / August 2012
- Published online by Cambridge University Press:
- 28 May 2015, pp. 204-213
- Print publication:
- August 2012
-
- Article
- Export citation
Nonlinear Multipoint Boundary Value Problems for Second Order Differential Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 3 / 01 September 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 475-490
- Print publication:
- 01 September 2010
-
- Article
-
- You have access
- Export citation
FURTHER RESULTS ON POSITIVE PERIODIC SOLUTIONS OF IMPULSIVE FUNCTIONAL DIFFERENTIAL EQUATIONS AND APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 27 July 2009, pp. 513-533
-
- Article
-
- You have access
- Export citation
NEW GRONWALL–OU-IANG TYPE INTEGRAL INEQUALITIES AND THEIR APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 111-127
-
- Article
-
- You have access
- Export citation
Discounted Optimal Stopping for Maxima of Some Jump-Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 713-731
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
POSITIVE INCREASING SOLUTIONS ON THE HALF-LINE TO SECOND ORDER NONLINEAR DELAY DIFFERENTIAL EQUATIONS
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 2 / May 2007
- Published online by Cambridge University Press:
- 09 August 2007, pp. 197-211
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
Existence results for differential equations with reflection of the argument
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-260
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation
A Topological Transversality Theorem For Multi-Valued Maps In Locally Convex Spaces With Applications To Neutral Equations
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 5 / 01 October 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1003-1013
- Print publication:
- 01 October 1992
-
- Article
-
- You have access
- Export citation
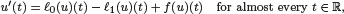
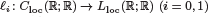 are linear positive continuous operators and
are linear positive continuous operators and 