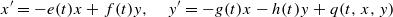Refine search
Actions for selected content:
19 results
Flocking dynamics of agents moving with a constant speed and a randomly switching topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 419-447
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eternal solutions to a porous medium equation with strong non-homogeneous absorption. Part I: radially non-increasing profiles
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 14 March 2024, pp. 1998-2019
- Print publication:
- December 2025
-
- Article
- Export citation
Resilience of dynamical systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 05 June 2023, pp. 155-200
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform moment propagation for the Becker--Döring equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 995-1015
- Print publication:
- August 2019
-
- Article
- Export citation
A Model of the Signal Transduction Process under a Delay
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 741-751
- Print publication:
- November 2017
-
- Article
- Export citation
On the Roughness of Quasinilpotency Property of One-parameter Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 364-371
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
Stable laws and Beurling kernels
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue A / July 2016
- Published online by Cambridge University Press:
- 25 July 2016, pp. 239-248
- Print publication:
- July 2016
-
- Article
- Export citation
Lyapunov Stability and Attraction Under Equivariant Maps
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1247-1269
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Bounds and algorithms for the
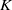 $K$ -Bessel function of imaginary order
$K$ -Bessel function of imaginary order
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 78-108
-
- Article
-
- You have access
- Export citation
Equivalence of Lp Stability and Exponential Stability of Nonlinear Lipschitzian Semigroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 882-889
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
On the Dichotomy of the Evolution Families: A Discrete-Argument Approach
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 3 / 01 September 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 527-537
- Print publication:
- 01 September 2011
-
- Article
-
- You have access
- Export citation
Lyapunov Theorems for the Asymptotic Behavior of Evolution Families on the Half-Line
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 2 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 364-369
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC INTEGRATION OF SECOND-ORDER NONLINEAR DIFFERENCE EQUATIONS
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 08 December 2010, pp. 223-243
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
THE GENERALISED LIÉNARD EQUATIONS
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 September 2009, pp. 605-617
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
CONVERGENCE OF SOLUTIONS OF TIME-VARYING LINEAR SYSTEMS WITH INTEGRABLE FORCING TERM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 445-462
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
ON ${\bf (a,b)}$-DICHOTOMY FOR EVOLUTIONARY PROCESSES ON A HALF-LINE
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 2 / May 2004
- Published online by Cambridge University Press:
- 19 May 2004, pp. 217-225
- Print publication:
- May 2004
-
- Article
-
- You have access
- Export citation
Urn models and differential algebraic equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 40 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 14 July 2016, pp. 401-412
- Print publication:
- June 2003
-
- Article
- Export citation
On the Injectivity of C 1 Maps of the Real Plane
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 6 / 01 December 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1187-1201
- Print publication:
- 01 December 2002
-
- Article
-
- You have access
- Export citation
Analyticity of iterates of random non-expansive maps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 193-220
- Print publication:
- March 2000
-
- Article
- Export citation












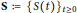
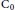
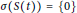
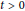
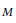
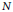
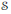
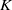
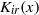
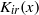

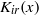
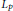
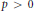
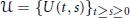
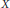
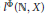
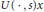
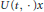
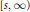
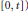
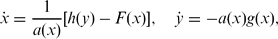
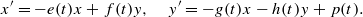
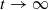 . Here, the zero solution of the corresponding homogeneous linear system is assumed to be neither uniformly stable nor uniformly attractive. Sufficient conditions are given for asymptotic stability of the zero solution of the nonlinear perturbed system
. Here, the zero solution of the corresponding homogeneous linear system is assumed to be neither uniformly stable nor uniformly attractive. Sufficient conditions are given for asymptotic stability of the zero solution of the nonlinear perturbed system