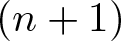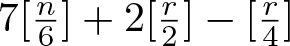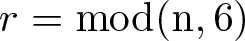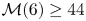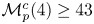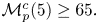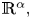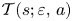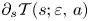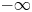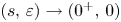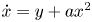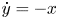Refine search
Actions for selected content:
13 results
Limit cycles near a nilpotent center and a homoclinic loop to a nilpotent singularity of Hamiltonian systems
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 October 2025, pp. 1-36
-
- Article
- Export citation
General study on limit cycle bifurcation near a double eight figure loop
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-17
-
- Article
- Export citation
Limit cycles in a rotated family of generalized Liénard systems allowing for finitely many switching lines
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 21 March 2024, pp. 2121-2149
- Print publication:
- December 2025
-
- Article
- Export citation
Cyclicity of rigid centres on centre manifolds of three-dimensional systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 188-200
- Print publication:
- February 2024
-
- Article
- Export citation
Cyclicity of period annulus for a class of quadratic reversible systems with a nonrational first integral
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 09 November 2022, pp. 1706-1728
- Print publication:
- October 2023
-
- Article
- Export citation
The local cyclicity problem: Melnikov method using Lyapunov constants
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 356-375
-
- Article
- Export citation
Non-bifurcation of critical periods from semi-hyperbolic polycycles of quadratic centres
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 01 December 2021, pp. 104-114
- Print publication:
- February 2023
-
- Article
- Export citation
The cyclicity of the period annulus of a reversible quadratic system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 February 2021, pp. 281-290
- Print publication:
- April 2022
-
- Article
- Export citation
On the birth and death of algebraic limit cycles in quadratic differential systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 317-336
-
- Article
- Export citation
On the Poincaré problem and Liouvillian integrability of quadratic Liénard differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 January 2020, pp. 3231-3251
- Print publication:
- December 2020
-
- Article
- Export citation
Limit Cycles of a Perturbation of a Polynomial Hamiltonian Systems of Degree 4 Symmetric with Respect to the Origin
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 547-561
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Hilbert’s 16th problem on a period annulus and Nash space of arcs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 377-409
- Print publication:
- September 2020
-
- Article
- Export citation
Bifurcations of Limit Cycles From Infinity in Quadratic Systems
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 5 / 01 October 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1064
- Print publication:
- 01 October 2002
-
- Article
-
- You have access
- Export citation