Refine search
Actions for selected content:
7 results
On the Square of the First Zero of the Bessel Function Jv(z)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 1 / 01 March 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 56-67
- Print publication:
- 01 March 1999
-
- Article
-
- You have access
- Export citation
Transient characteristics of an M/M/∞ system
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 862-888
- Print publication:
- September 1995
-
- Article
- Export citation
A Unimodal Property of Purely Imaginary Zeros of Bessel and Related Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 3 / 01 September 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 365-373
- Print publication:
- 01 September 1994
-
- Article
-
- You have access
- Export citation
A Class of Generalized Hypergeometric Functions in Several Variables
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 6 / 01 December 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1317-1338
- Print publication:
- 01 December 1992
-
- Article
-
- You have access
- Export citation
Inflection Points of Bessel Functions of Negative Order
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 6 / 01 December 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1309-1322
- Print publication:
- 01 December 1991
-
- Article
-
- You have access
- Export citation
On the Points of Inflection of Bessel Functions of Positive Order, II
-
- Journal:
- Canadian Journal of Mathematics / Volume 43 / Issue 3 / 01 June 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 628-651
- Print publication:
- 01 June 1991
-
- Article
-
- You have access
- Export citation
A Note on Completely and Absolutely Monotone Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 2 / 01 June 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 143-148
- Print publication:
- 01 June 1982
-
- Article
-
- You have access
- Export citation
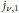
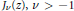

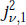
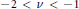
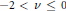
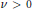
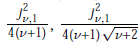
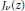
 is unimodal on (
is unimodal on ( .
.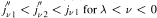 and
and 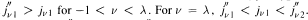 . Moreover,
. Moreover, 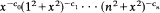 completely monotone?”
completely monotone?”