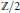Refine search
Actions for selected content:
7 results
OBSTRUCTIONS TO ALGEBRAIZING TOPOLOGICAL VECTOR BUNDLES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 21 March 2019, e6
-
- Article
-
- You have access
- Open access
- Export citation
Moduli Spaces of Vector Bundles over a Real Curve: ℤ/2-Betti Numbers
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 5 / 01 October 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-992
- Print publication:
- 01 October 2014
-
- Article
-
- You have access
- Export citation
On Segre Forms of Positive Vector Bundles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 108-113
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
Connections on a Parabolic Principal Bundle, II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 2 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 175-185
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
Connections on a Parabolic Principal Bundle Over a Curve
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 2 / 01 April 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 262-281
- Print publication:
- 01 April 2006
-
- Article
-
- You have access
- Export citation
Harder–Narasimhan reduction of a principal bundle
-
- Journal:
- Nagoya Mathematical Journal / Volume 174 / 2004
- Published online by Cambridge University Press:
- 22 January 2016, pp. 201-223
- Print publication:
- 2004
-
- Article
-
- You have access
- Export citation
ON HOLOMORPHIC PRINCIPAL BUNDLES OVER A COMPACT RIEMANN SURFACE ADMITTING A FLAT CONNECTION, II
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 4 / July 2003
- Published online by Cambridge University Press:
- 09 June 2003, pp. 440-444
- Print publication:
- July 2003
-
- Article
- Export citation