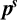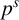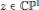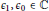Refine search
Actions for selected content:
3 results
GHOSTS AND CONGRUENCES FOR
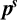 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
- Print publication:
- February 2024
-
- Article
- Export citation
The Bifurcation Diagram of Cubic Polynomial Vector Fields on CP1
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 381-401
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Open access
- Export citation
Isomonodromic deformation of Fuchsian projective connections on elliptic curves
-
- Journal:
- Nagoya Mathematical Journal / Volume 171 / 2003
- Published online by Cambridge University Press:
- 22 January 2016, pp. 127-161
- Print publication:
- 2003
-
- Article
-
- You have access
- Export citation