Refine search
Actions for selected content:
6 results
Trigonometric convexity of the multidimensional indicator
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 January 2024, pp. 384-399
- Print publication:
- April 2025
-
- Article
- Export citation
EXTENSION AND RESTRICTION FOR BERGMAN SCALE OF SPACES AND ONE-DIMENSIONAL SUBVARIETIES ON CONVEX FINITE TYPE DOMAINS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 221 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 15 March 2016, pp. 165-183
- Print publication:
- March 2016
-
- Article
-
- You have access
- HTML
- Export citation
DIFFERENCES OF COMPOSITION OPERATORS ON THE BLOCH SPACE IN THE POLYDISC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-471
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Growth Spaces and Growth Norm Estimates for
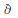 on Convex Domains of Finite Type
on Convex Domains of Finite Type
-
- Journal:
- Canadian Mathematical Bulletin / Volume 49 / Issue 4 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 508-525
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation
Lp extension of holomorphic functions from submanifolds to strictly pseudoconvex domains with non-smooth boundary
-
- Journal:
- Nagoya Mathematical Journal / Volume 172 / 2003
- Published online by Cambridge University Press:
- 22 January 2016, pp. 103-110
- Print publication:
- 2003
-
- Article
-
- You have access
- Export citation
Zero varieties for the Nevanlinna class on all convex domains of finite type
-
- Journal:
- Nagoya Mathematical Journal / Volume 163 / September 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 215-227
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation
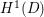
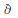 on Convex Domains of Finite Type
on Convex Domains of Finite Type
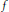
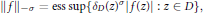
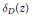

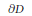
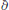
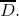 . Then any
. Then any 