No CrossRef data available.
Article contents
Lp extension of holomorphic functions from submanifolds to strictly pseudoconvex domains with non-smooth boundary
Published online by Cambridge University Press: 22 January 2016
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let D be a bounded strictly pseudoconvex domain in ℂn (with not necessarily smooth boundary) and let X be a submanifold in a neighborhood of 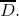 . Then any Lp (1 ≥ p < ∞) holomorphic function in X ∩ D can be extended to an Lp holomorphic function in D.
. Then any Lp (1 ≥ p < ∞) holomorphic function in X ∩ D can be extended to an Lp holomorphic function in D.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 2003
References
[1]
Beatrous, F., Lp estimates for extensions of holomorphic functions, Michigan Math. J., 32 (1985), 361–380.Google Scholar
[2]
Cho, H. R., A counterexample to the Lp extension of holomorphic functions from subvarieties to pseudoconvex domains, Complex Variables, 35 (1998), 89–91.Google Scholar
[3]
Cumenge, A., Extension dan des classes de Hardy de fonctions holomorphes et estimations de type “mesures de Carleson” pour l’equation ∂, Ann. Inst. Fourier, 33 (1983), 59–97.Google Scholar
[4]
Henkin, G. M., Continuation of bounded holomorphic functions from submanifolds in general position in a strictly pseudoconvex domain, Math. USSR Izv., 6 (1972), 536–563.Google Scholar
[5]
Henkin, G. M. and Leiterer, J., Theory of functions on complex manifolds, Birkhäuser, 1984.Google Scholar
[6]
Ohsawa, T. and Takegoshi, K., On the extension of L2 holomorphic functions, Math. Z., 195 (1987), 197–204.Google Scholar
[7]
Schmalz, G., Solution of the
 -equation with uniform estimates on strictly q-convex domains with non-smooth boundary, Math. Z., 202 (1989), 409–430.Google Scholar
-equation with uniform estimates on strictly q-convex domains with non-smooth boundary, Math. Z., 202 (1989), 409–430.Google Scholar

