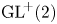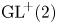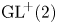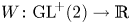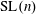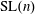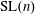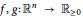Refine search
Actions for selected content:
18 results
Additive kinematic formulas for convex functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal transport through a toll station
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 18 September 2024, pp. 613-637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A rank-one convex, nonpolyconvex isotropic function on
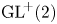 $\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
$\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 February 2022, pp. 356-381
- Print publication:
- April 2022
-
- Article
- Export citation
INEQUALITIES FOR DRAGOMIR’S MAPPINGS VIA STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 240-250
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
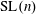 $\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
$\text{SL}(n)$ Invariant Valuations on Super-Coercive Convex Functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 25 October 2019, pp. 108-130
- Print publication:
- February 2021
-
- Article
- Export citation
Orlicz Addition for Measures and an Optimization Problem for the
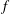 $f$-divergence
$f$-divergence
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 455-479
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 June 2019, pp. 2620-2631
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
CHARACTERIZATIONS OF QUASICONVEX AND PSEUDOCONVEX FUNCTIONS BY THEIR SECOND-ORDER REGULAR SUBDIFFERENTIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 217-229
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Rank-one convexity implies polyconvexity for isotropic, objective and isochoric elastic energies in the two-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 18 May 2017, pp. 571-597
- Print publication:
- June 2017
-
- Article
- Export citation
On a Linear Refinement of the Prékopa-Leindler Inequality
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 4 / 01 August 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 762-783
- Print publication:
- 01 August 2016
-
- Article
-
- You have access
- Export citation
Convex Functions on Discrete Time Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-233
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
CONCAVITY PROPERTIES OF EXTENSIONS OF THE PARALLEL VOLUME
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 13 January 2015, pp. 266-282
- Print publication:
- 2016
-
- Article
- Export citation
General convex stochastic orderings and related martingale-type structures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 105-127
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
seven views on approximate convexity and the geometry of $k$-spaces
-
- Journal:
- Journal of the London Mathematical Society / Volume 72 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 04 October 2005, pp. 457-477
- Print publication:
- October 2005
-
- Article
- Export citation
HESSIAN MEASURES OF CONVEX FUNCTIONS AND APPLICATIONS TO AREA MEASURES
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 04 February 2005, pp. 221-235
- Print publication:
- February 2005
-
- Article
- Export citation
ON APPROXIMATELY MIDCONVEX FUNCTIONS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 28 April 2004, pp. 339-350
- Print publication:
- May 2004
-
- Article
- Export citation
Two gradient properties of explicitly convex functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 404-410
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
Generalized Second Fundamental form for Lipschitzian Hypersurfaces by Way of Second Epi Derivatives
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 4 / 01 December 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 523-536
- Print publication:
- 01 December 1992
-
- Article
-
- You have access
- Export citation