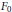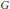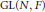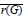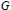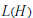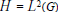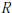Refine search
Actions for selected content:
4 results
On homological properties of the Schlichting completion
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 04 September 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Types for Unramified p-Adic Unitary Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1067-1107
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
The Operator Biprojectivity of the Fourier Algebra
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 5 / 01 October 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1100-1120
- Print publication:
- 01 October 2002
-
- Article
-
- You have access
- Export citation
The Right Regular Representation of a Compact Right Topological Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 4 / 01 December 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 463-472
- Print publication:
- 01 December 1998
-
- Article
-
- You have access
- Export citation