Article contents
The Right Regular Representation of a Compact Right Topological Group
Published online by Cambridge University Press: 20 November 2018
Abstract
We show that for certain compact right topological groups, 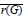 $\overline{r(G)}$ , the strong operator topology closure of the image of the right regular representation of
$\overline{r(G)}$ , the strong operator topology closure of the image of the right regular representation of 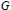 $G$ in
$G$ in 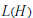 $L(H)$ , where
$L(H)$ , where 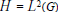 $H\,=\,{{L}^{2}}\,(G)$ , is a compact topological group and introduce a class of representations,
$H\,=\,{{L}^{2}}\,(G)$ , is a compact topological group and introduce a class of representations, 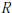 $R$ , which effectively transfers the representation theory of
$R$ , which effectively transfers the representation theory of 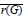 $\overline{r(G)}$ over to
$\overline{r(G)}$ over to 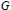 $G$ . Amongst the groups for which this holds is the class of equicontinuous groups which have been studied by Ruppert in [10].We use familiar examples to illustrate these features of the theory and to provide a counter-example. Finally we remark that every equicontinuous group which is at the same time a Borel group is in fact a topological group.
$G$ . Amongst the groups for which this holds is the class of equicontinuous groups which have been studied by Ruppert in [10].We use familiar examples to illustrate these features of the theory and to provide a counter-example. Finally we remark that every equicontinuous group which is at the same time a Borel group is in fact a topological group.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 2
- Cited by

