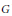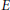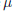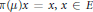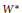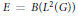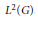Refine search
Actions for selected content:
2 results
Approximate homomorphisms and sofic approximations of orbit equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 3455-3480
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Choquet–Deny Equation in a Banach Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 795-827
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation