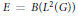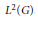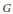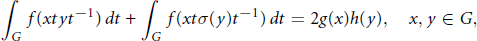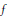Refine search
Actions for selected content:
5 results
RADU GROUPS ACTING ON TREES ARE CCR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 149-186
- Print publication:
- October 2024
-
- Article
- Export citation
The Choquet–Deny Equation in a Banach Space
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 4 / 01 August 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 795-827
- Print publication:
- 01 August 2007
-
- Article
-
- You have access
- Export citation
SYMMETRY OF WEIGHTED $L{\uppercase{\footnotesize{L^1}}}$-ALGEBRAS AND THE GRS-CONDITION
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 4 / August 2006
- Published online by Cambridge University Press:
- 24 July 2006, pp. 625-635
- Print publication:
- August 2006
-
- Article
- Export citation
On the Generalized d’Alembert's and Wilson's Functional Equations on a Compact Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 4 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 505-522
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
Dilations of one Parameter Semigroups of Positive Contractions on Lp Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 4 / 01 August 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 736-748
- Print publication:
- 01 August 1997
-
- Article
-
- You have access
- Export citation