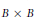Refine search
Actions for selected content:
10 results
A CHARACTERISATION OF SEMIGROUPS WITH ONLY COUNTABLY MANY SUBDIRECT PRODUCTS WITH
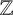 $\mathbb {Z}$
$\mathbb {Z}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 314-323
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On minimal ideals in pseudo-finite semigroups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 2007-2037
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semigroups whose right ideals are finitely generated
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 01 October 2021, pp. 848-883
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete regularity of Ellis semigroups of
 $\mathbb{Z} $-actions
$\mathbb{Z} $-actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 3593-3609
- Print publication:
- December 2021
-
- Article
- Export citation
Twisted Brauer monoids
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 10 April 2018, pp. 731-750
- Print publication:
- August 2018
-
- Article
- Export citation
Uniform Bands
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 3 / October 2014
- Published online by Cambridge University Press:
- 18 July 2014, pp. 575-587
-
- Article
-
- You have access
- Export citation
Expansions of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-228
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
CONGRUENCES ON MONOIDS OF ORDER-PRESERVING OR ORDER-REVERSING TRANSFORMATIONS ON A FINITE CHAIN
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue 2 / May 2005
- Published online by Cambridge University Press:
- 27 July 2005, pp. 413-424
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
An Explicit Cell Decomposition of the Wonderful Compactification of a Semisimple Algebraic Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 1 / 01 March 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 140-148
- Print publication:
- 01 March 2003
-
- Article
-
- You have access
- Export citation
On existence varieties of orthodox semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-125
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
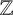



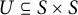
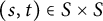
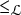
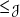
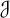
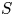
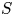
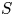
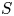
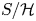

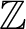
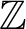
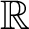
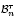 , comparing and contrasting it with the structure of the (untwisted) Brauer monoid
, comparing and contrasting it with the structure of the (untwisted) Brauer monoid 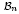 . We characterize Green's relations and pre-orders on
. We characterize Green's relations and pre-orders on