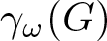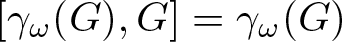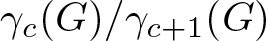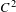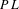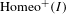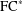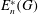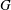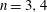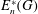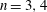Refine search
Actions for selected content:
14 results
On the degree-two part of the associated graded of the lower central series of the Torelli group
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 20 October 2025, pp. 1-39
-
- Article
- Export citation
On the structures of the Johnson cokernels of the basis-conjugating automorphism groups of free groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-29
-
- Article
- Export citation
Baumslag–Solitar groups and residual nilpotence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 532-547
-
- Article
- Export citation
GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 276-283
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower central series, surface braid groups, surjections and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 373-399
- Print publication:
- March 2022
-
- Article
- Export citation
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation
ABELIAN AND METABELIAN QUOTIENT GROUPS OF SURFACE BRAID GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 119-142
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
ON GENERALISED FC-GROUPS IN WHICH NORMALITY IS A TRANSITIVE RELATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 29 October 2015, pp. 192-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF P. HALL FOR ENGEL WORDS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 237-246
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Approximating the Schur multiplier of certain infinitely presented groups via nilpotent quotients
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 260-271
-
- Article
-
- You have access
- Export citation
NEW OBSTRUCTIONS FOR THE SURJECTIVITY OF THE JOHNSON HOMOMORPHISM OF THE AUTOMORPHISM GROUP OF A FREE GROUP
-
- Journal:
- Journal of the London Mathematical Society / Volume 74 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 25 October 2006, pp. 341-360
- Print publication:
- October 2006
-
- Article
- Export citation
An Embedding Construction for Ordered Groups: To Professor Alexander Yurievich Ol'shanskii, my teacher
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 379-392
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Groups whose proper quotients are hypercentral
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 224-237
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
On the lower central factors of free centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-75
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation