We define higher semiadditive algebraic K-theory, a variant of algebraic K-theory that takes into account higher semiadditive structure, as enjoyed for example by the $\mathrm {K}(n)$- and $\mathrm {T}(n)$-local categories. We prove that it satisfies a form of the redshift conjecture. Namely, that if $R$ is a ring spectrum of height $\leq n$, then its semiadditive K-theory is of height $\leq n+1$. Under further hypothesis on $R$, which are satisfied for example by the Lubin–Tate spectrum $\mathrm {E}_n$, we show that its semiadditive algebraic K-theory is of height exactly $n+1$. Finally, we connect semiadditive K-theory to $\mathrm {T}(n+1)$-localized K-theory, showing that they coincide for any $p$-invertible ring spectrum and for the completed Johnson–Wilson spectrum $\widehat {\mathrm {E}(n)}$.

We prove that real topological Hochschild homology $\mathrm {THR}$ for schemes with involution satisfies base change and descent for the ${\mathbb {Z}/2}$-isovariant étale topology. As an application, we provide computations for the projective line (with and without involution) and the higher-dimensional projective spaces.

In this paper we compute the topological Hochschild homology of quotients of discrete valuation rings (DVRs). Along the way we give a short argument for Bökstedt periodicity and generalizations over various other bases. Our strategy also gives a very efficient way to redo the computations of $\operatorname {THH}$ (respectively, logarithmic $\operatorname {THH}$) of complete DVRs originally due to Lindenstrauss and Madsen (respectively, Hesselholt and Madsen).

For a not-necessarily commutative ring $R$ we define an abelian group $W(R;M)$ of Witt vectors with coefficients in an $R$-bimodule $M$. These groups generalize the usual big Witt vectors of commutative rings and we prove that they have analogous formal properties and structure. One main result is that $W(R) := W(R;R)$ is Morita invariant in $R$. For an $R$-linear endomorphism $f$ of a finitely generated projective $R$-module we define a characteristic element $\chi _f \in W(R)$. This element is a non-commutative analogue of the classical characteristic polynomial and we show that it has similar properties. The assignment $f \mapsto \chi _f$ induces an isomorphism between a suitable completion of cyclic $K$-theory $K_0^{\mathrm {cyc}}(R)$ and $W(R)$.

We give counterexamples to the degeneration of the Hochschild-Kostant-Rosenberg spectral sequence in characteristic p, both in the untwisted and twisted settings. We also prove that the de Rham-HP and crystalline-TP spectral sequences need not degenerate.

Vorst's conjecture relates the regularity of a ring with the $\mathbb {A}^{1}$-homotopy invariance of its $K$-theory. We show a variant of this conjecture in positive characteristic.

We discuss some general properties of $\mathrm {TR}$ and its $K(1)$-localization. We prove that after $K(1)$-localization, $\mathrm {TR}$ of $H\mathbb {Z}$-algebras is a truncating invariant in the Land–Tamme sense, and deduce $h$-descent results. We show that for regular rings in mixed characteristic, $\mathrm {TR}$ is asymptotically $K(1)$-local, extending results of Hesselholt and Madsen. 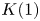As an application of these methods and recent advances in the theory of cyclotomic spectra, we construct an analog of Thomason's spectral sequence relating $K(1)$-local $K$-theory and étale cohomology for $K(1)$-local 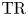$\mathrm {TR}$.

Let X be a simply connected closed oriented manifold of rationally elliptic homotopy type. We prove that the string topology bracket on the $S^1$-equivariant homology $ {\overline {\text {H}}}_\ast ^{S^1}({\mathcal {L}} X,{\mathbb {Q}}) $ of the free loop space of X preserves the Hodge decomposition of $ {\overline {\text {H}}}_\ast ^{S^1}({\mathcal {L}} X,{\mathbb {Q}}) $, making it a bigraded Lie algebra. We deduce this result from a general theorem on derived Poisson structures on the universal enveloping algebras of homologically nilpotent finite-dimensional DG Lie algebras. Our theorem settles a conjecture of [7].

Fundamental group of a manifold gives a deep effect on its underlying smooth structure. In this paper we introduce a new variant of the Donaldson invariant in Yang–Mills gauge theory from twisting by the Picard group of a 4-manifold in the case when the fundamental group is free abelian. We then generalise it to the general case of fundamental groups by use of the framework of non commutative geometry. We also verify that our invariant distinguishes smooth structures between some homeomorphic 4-manifolds.

In this paper we prove a categorification of the Grothendieck–Riemann–Roch theorem. Our result implies in particular a Grothendieck–Riemann–Roch theorem for Toën and Vezzosi's secondary Chern character. As a main application, we establish a comparison between the Toën–Vezzosi Chern character and the classical Chern character, and show that the categorified Chern character recovers the classical de Rham realization.

We construct a Baum–Connes assembly map localised at the unit element of a discrete group $\Gamma$. This morphism, called $\mu _\tau$, is defined in $KK$-theory with coefficients in $\mathbb {R}$ by means of the action of the idempotent $[\tau ]\in KK_{\mathbin {{\mathbb {R}}}}^\Gamma (\mathbb {C},\mathbb {C})$ canonically associated to the group trace of $\Gamma$. We show that the corresponding $\tau$-Baum–Connes conjecture is weaker than the classical version, but still implies the strong Novikov conjecture. The right-hand side of $\mu _\tau$ is functorial with respect to the group $\Gamma$.

In this paper we show that to a unital associative algebra object (resp. co-unital co-associative co-algebra object) of any abelian monoidal category ($\mathscr{C},\otimes$) endowed with a symmetric 2-trace, i.e., an $F\in \text{Fun}(\mathscr{C},\text{Vec})$ satisfying some natural trace-like conditions, one can attach a cyclic (resp. cocyclic) module, and therefore speak of the (co)cyclic homology of the (co)algebra “with coefficients in $F$”. Furthermore, we observe that if $\mathscr{M}$ is a $\mathscr{C}$-bimodule category and $(F,M)$ is a stable central pair, i.e., $F\in \text{Fun}(\mathscr{M},\text{Vec})$ and $M\in \mathscr{M}$ satisfy certain conditions, then $\mathscr{C}$ acquires a symmetric 2-trace. The dual notions of symmetric 2-contratraces and stable central contrapairs are derived as well. As an application we can recover all Hopf cyclic type (co)homology theories.

We develop a theory of $R$-module Thom spectra for a commutative symmetric ring spectrum $R$ and we analyze their multiplicative properties. As an interesting source of examples, we show that $R$-algebra Thom spectra associated to the special unitary groups can be described in terms of quotient constructions on $R$. We apply the general theory to obtain a description of the $R$-based topological Hochschild homology associated to an $R$-algebra Thom spectrum.

We provide an explicit formula for the generalized cyclic shuffle map for cylindrical modules. Using this formula we give a combinatorial proof of the generalized cyclic Eilenberg–Zilber theorem.

Let $k$ be a base commutative ring, $R$ a commutative ring of coefficients, $X$ a quasi-compact quasi-separated $k$-scheme, and $A$ a sheaf of Azumaya algebras over $X$ of rank $r$. Under the assumption that $1/r\in R$, we prove that the noncommutative motives with $R$-coefficients of $X$ and $A$ are isomorphic. As an application, we conclude that a similar isomorphism holds for every $R$-linear additive invariant. This leads to several computations. Along the way we show that, in the case of finite-dimensional algebras of finite global dimension, all additive invariants are nilinvariant.

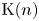
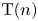
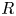
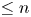
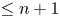
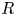
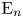
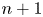
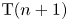
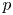
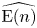
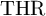
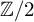
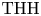
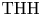
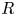
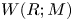
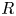
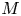
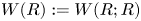
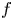
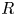
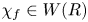
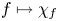
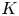
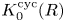
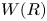
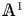
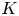
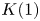
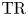
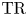
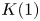
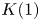
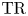
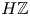
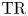
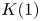
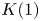
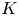
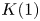
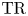
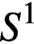
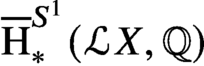
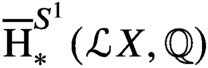
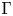
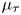
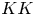
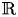
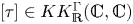
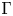
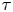
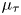
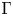
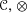
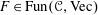
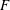
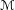
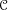
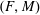
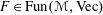
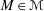
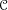
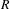
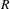
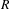
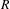
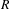
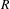
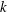
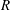
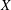
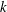
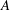
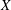
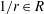
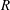
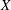
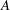
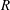
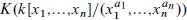We consider the algebraic K-theory of a truncated polynomial algebra in several commuting variables, . This naturally leads to a new generalization of the big Witt vectors. If k is a perfect field of positive characteristic we describe the K-theory computation in terms of a cube of these Witt vectors on ℕn. If the characteristic of k does not divide any of the ai we compute the K-groups explicitly. We also compute the K-groups modulo torsion for k = ℤ.

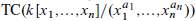To understand this K-theory spectrum we use the cyclotomic trace map to topological cyclic homology, and write as the iterated homotopy cofiber of an n-cube of spectra, each of which is easier to understand.

In this paper we study the cyclic cohomology of certain ×-Hopf algebras: universal enveloping algebras, quantum algebraic tori, the Connes-Moscovici ×-Hopf algebroids and the Kadison bialgebroids. Introducing their stable anti Yetter-Drinfeld modules and cocyclic modules, we compute their cyclic cohomology. Furthermore, we provide a pairing for the cyclic cohomology of ×-Hopf algebras which generalizes the Connes-Moscovici characteristic map to ×-Hopf algebras. This enables us to transfer the ×-Hopf algebra cyclic cocycles to algebra cyclic cocycles.

We construct a duality isomorphism in equivariant periodic cyclic homology analogous to Baaj-Skandalis duality in equivariant Kasparov theory. As a consequence we obtain general versions of the Green-Julg theorem and the dual Green-Julg theorem in periodic cyclic theory.

Throughout we work within the framework of bornological quantum groups, thus in particular incorporating at the same time actions of arbitrary classical Lie groups as well as actions of compact or discrete quantum groups. An important ingredient in the construction of our duality isomorphism is the notion of a modular pair for a bornological quantum group, closely related to the concept introduced by Connes and Moscovici in their work on cyclic cohomology for Hopf algebras.

In this article, we further the study of higher K-theory of differential graded (dg) categories via universal invariants, initiated in [G. Tabuada, Higher K-theory via universal invariants, Duke Math. J. 145 (2008), 121–206]. Our main result is the co-representability of non-connective K-theory by the base ring in the ‘universal localizing motivator’. As an application, we obtain for free higher Chern characters, respectively higher trace maps, from non-connective K-theory to cyclic homology, respectively to topological Hochschild homology.

We describe explicitly the Voevodsky's triangulated category of motives (and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DMgm ℚ is (anti)isomorphic to Hanamura's (k).

We obtain a description of all subcategories (including those of Tate motives) and of all localizations of . We construct a conservative weight complex functor ; t gives an isomorphism . A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if tℚ is an equivalence.

For a realization D of we construct a spectral sequence S (the spectral sequence of motivic descent) converging to the cohomology of an arbitrary motif X. S is ‘motivically functorial’; it gives a canonical functorial weight filtration on the cohomology of D(X). For the ‘standard’ realizations this filtration coincides with the usual one (up to a shift of indices). For the motivic cohomology this weight filtration is non-trivial and appears to be quite new.

We define the (rational) length of a motif M; modulo certain ‘standard’ conjectures this length coincides with the maximal length of the weight filtration of the singular cohomology of M.