7 results
Ample Groupoids, Topological Full groups, Algebraic K-theory Spectra and Infinite Loop Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 February 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALISATIONS OF LODAY’S ASSEMBLY MAPS FOR LAWVERE’S ALGEBRAIC THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 22 February 2023, pp. 811-837
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 April 2020, pp. 115-144
- Print publication:
- February 2022
-
- Article
- Export citation
Smoothness in Relative Geometry
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 November 2013, pp. 461-491
- Print publication:
- December 2013
-
- Article
- Export citation
from mapping class groups to automorphism groups of free groups
-
- Journal:
- Journal of the London Mathematical Society / Volume 72 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 04 October 2005, pp. 510-524
- Print publication:
- October 2005
-
- Article
- Export citation
THE CYCLOTOMIC TRACE FOR S-ALGEBRAS
-
- Journal:
- Journal of the London Mathematical Society / Volume 70 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 03 December 2004, pp. 659-677
- Print publication:
- December 2004
-
- Article
- Export citation

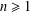
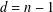
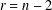
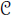 ⊗1). In this article, we define a notion of smoothness in this relative (and not necessarily additive) context which generalizes the notion of smoothness in the category of rings. This generalisation consists in replacing homological finiteness conditions by homotopical ones, using the Dold-Kan correspondence. To do this, we provide the category
⊗1). In this article, we define a notion of smoothness in this relative (and not necessarily additive) context which generalizes the notion of smoothness in the category of rings. This generalisation consists in replacing homological finiteness conditions by homotopical ones, using the Dold-Kan correspondence. To do this, we provide the category 