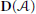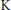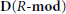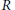Refine search
Actions for selected content:
5 results
A COCOMPLETE BUT NOT COMPLETE ABELIAN CATEGORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 442-445
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A Candidate for the Abelian Category of Mixed Elliptic Motives
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 November 2013, pp. 569-600
- Print publication:
- December 2013
-
- Article
- Export citation
GOLDIE DIMENSION, DUAL KRULL DIMENSION AND SUBDIRECT IRREDUCIBILITY
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue A / July 2010
- Published online by Cambridge University Press:
- 24 June 2010, pp. 19-32
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
DERIVED FUNCTORS OF INVERSE LIMITS REVISITED
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 65-83
- Print publication:
- February 2006
-
- Article
- Export citation
Localization in Categories of Complexes and Unbounded Resolutions
-
- Journal:
- Canadian Journal of Mathematics / Volume 52 / Issue 2 / 01 April 2000
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-247
- Print publication:
- 01 April 2000
-
- Article
-
- You have access
- Export citation