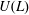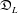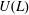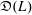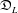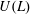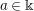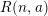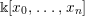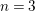Refine search
Actions for selected content:
9 results
Graded extensions of Verma modules
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 285-311
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Free Group Algebras in Division Rings with Valuation II
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 05 July 2019, pp. 1463-1504
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
THE CURVED A∞-COALGEBRA OF THE KOSZUL CODUAL OF A FILTERED DG ALGEBRA
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 31 August 2018, pp. 575-600
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A NEW FAMILY OF POISSON ALGEBRAS AND THEIR DEFORMATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 25 September 2017, pp. 32-86
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON THE SMOOTHNESS OF CENTRES OF RATIONAL CHEREDNIK ALGEBRAS IN POSITIVE CHARACTERISTIC
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue A / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 27-54
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
THE ASSOCIATED VARIETY OF A POISSON PRIME IDEAL
-
- Journal:
- Journal of the London Mathematical Society / Volume 72 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 20 July 2005, pp. 110-120
- Print publication:
- August 2005
-
- Article
- Export citation
Dualizing complexes and perverse modules over differential algebras
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 3 / May 2005
- Published online by Cambridge University Press:
- 21 April 2005, pp. 620-654
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
KOSTANT'S THEOREM FOR SPECIAL FILTERED ALGEBRAS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 2 / March 2005
- Published online by Cambridge University Press:
- 10 March 2005, pp. 187-199
- Print publication:
- March 2005
-
- Article
- Export citation
Démonstration constructive de l'existence de polynômes de Bernstein–Sato pour plusieurs fonctions analytiques
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 01 December 2004, pp. 175-191
- Print publication:
- January 2005
-
- Article
-
- You have access
- Export citation