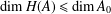Refine search
Actions for selected content:
2 results
ON GRADED SYMMETRIC CELLULAR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 349-362
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Group Actions on Quasi-Baer Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 4 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 564-582
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation