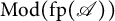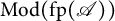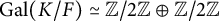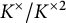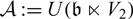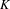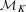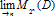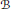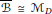Refine search
Actions for selected content:
23 results
Locally finitely presented Grothendieck categories and the pure semisimplicity conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-27
-
- Article
- Export citation
GRAPH CHARACTERISATION OF THE ANNIHILATOR IDEALS OF LEAVITT PATH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 498-507
- Print publication:
- December 2024
-
- Article
- Export citation
Galois module structure of square power classes for biquadratic extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 804-827
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 August 2021, pp. 248-256
- Print publication:
- April 2022
-
- Article
- Export citation
Coxeter Diagrams and the Köthe’s Problem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 656-686
- Print publication:
- June 2021
-
- Article
- Export citation
THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(𝔟⋉V2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. S77-S98
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Sylvester matrix rank functions on crossed products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 2913-2946
- Print publication:
- November 2020
-
- Article
- Export citation
The Universal Enveloping Algebra of the Schrödinger Algebra and its Prime Spectrum
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 4 / 01 December 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 688-703
- Print publication:
- 01 December 2018
-
- Article
-
- You have access
- Export citation
Uniqueness of the von Neumann Continuous Factor
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-982
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
GRADED CHAIN CONDITIONS AND LEAVITT PATH ALGEBRAS OF NO-EXIT GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 12 December 2017, pp. 229-256
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
RINGS WHOSE CYCLIC MODULES ARE DIRECT SUMS OF EXTENDING MODULES
-
- Journal:
- Glasgow Mathematical Journal / Volume 54 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 30 March 2012, pp. 605-617
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
RINGS OVER WHICH CYCLICS ARE DIRECT SUMS OF PROJECTIVE AND CS OR NOETHERIAN*
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue A / July 2010
- Published online by Cambridge University Press:
- 24 June 2010, pp. 103-110
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
POOR MODULES: THE OPPOSITE OF INJECTIVITY
-
- Journal:
- Glasgow Mathematical Journal / Volume 52 / Issue A / July 2010
- Published online by Cambridge University Press:
- 24 June 2010, pp. 7-17
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
2-Clean Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 145-153
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
CENTRES OF SKEWFIELDS AND COMPLETELY FAITHFUL IWASAWA MODULES
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 18 March 2008, pp. 457-468
- Print publication:
- July 2008
-
- Article
- Export citation
A STUDY OF UNIFORM ONE-SIDED IDEALS IN SIMPLE RINGS
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 September 2007, pp. 489-495
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Infinite Dimensional Representations of Canonical Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 1 / 01 February 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 180-224
- Print publication:
- 01 February 2006
-
- Article
-
- You have access
- Export citation
Modules which are invariant under monomorphisms of their injective hulls
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-360
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
PURE-PROJECTIVE MODULES
-
- Journal:
- Journal of the London Mathematical Society / Volume 71 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 06 April 2005, pp. 304-320
- Print publication:
- April 2005
-
- Article
- Export citation
A Simple Ring over which Proper Cyclics are Continuous is a PCI-Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 3 / 01 September 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 261-266
- Print publication:
- 01 September 1998
-
- Article
-
- You have access
- Export citation