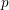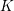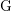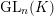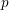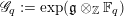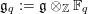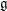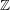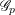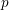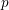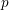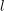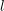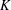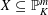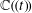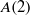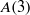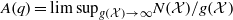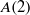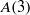Refine search
Actions for selected content:
8 results
Kirillov’s orbit method and polynomiality of the faithful dimension of
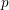 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 1618-1654
- Print publication:
- August 2019
-
- Article
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
FORMS OF DIFFERING DEGREES OVER NUMBER FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 92-123
- Print publication:
- 2017
-
- Article
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
On lower bounds for the Ihara constants
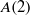 $A(2)$ and
$A(2)$ and 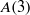 $A(3)$
$A(3)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1108-1128
- Print publication:
- July 2013
-
- Article
- Export citation
THE DENSITY OF RATIONAL POINTS ON NON-SINGULAR HYPERSURFACES, II
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 93 / Issue 2 / September 2006
- Published online by Cambridge University Press:
- 07 August 2006, pp. 273-303
- Print publication:
- September 2006
-
- Article
- Export citation
THE DENSITY OF RATIONAL POINTS ON NON-SINGULAR HYPERSURFACES, I
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 31 May 2006, pp. 401-410
- Print publication:
- June 2006
-
- Article
- Export citation