Refine search
Actions for selected content:
13 results
The Log Product Formula in Quantum K-theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 225-252
- Print publication:
- September 2023
-
- Article
- Export citation
The complexity of higher Chow groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 29 July 2022, pp. 903-911
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A weak Lefschetz result for Chow groups of complete intersections
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1014-1023
- Print publication:
- December 2021
-
- Article
- Export citation
LOCALIZATION BY
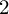 $2$-PERIODIC COMPLEXES AND VIRTUAL STRUCTURE SHEAVES
$2$-PERIODIC COMPLEXES AND VIRTUAL STRUCTURE SHEAVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1477-1506
- Print publication:
- September 2022
-
- Article
- Export citation
Localizing virtual structure sheaves for almost perfect obstruction theories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 07 December 2020, e61
-
- Article
-
- You have access
- Open access
- Export citation
ISOMORPHISMS UP TO BOUNDED TORSION BETWEEN RELATIVE
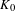 $K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS
$K_{0}$-GROUPS AND CHOW GROUPS WITH MODULUS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 1947-1968
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
CHERN CLASSES WITH MODULUS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 84-133
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
The Coniveau Filtration on
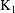 $\text{K}_{1}$ for Some Severi–Brauer Varieties
$\text{K}_{1}$ for Some Severi–Brauer Varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 24 October 2018, pp. 565-576
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Hochster's theta pairing and numerical equivalence
-
- Journal:
- Journal of K-Theory / Volume 14 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 28 July 2014, pp. 495-525
- Print publication:
- December 2014
-
- Article
- Export citation
Cycles de codimension 2 et H3 non ramifié pour les variétés sur les corps finis
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 04 February 2013, pp. 1-53
- Print publication:
- February 2013
-
- Article
- Export citation
Néron models and limits of Abel–Jacobi mappings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 288-366
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
The Abel–Jacobi map for higher Chow groups
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 13 March 2006, pp. 374-396
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Existence of vector bundles and global resolutions for singular surfaces
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 717-728
- Print publication:
- May 2004
-
- Article
-
- You have access
- Export citation
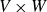
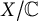
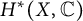
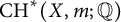
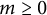
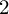
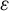
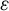
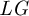
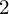
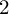
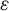
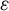
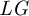

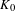
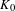

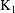
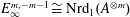
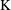
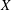
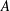
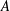
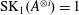
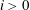
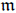 ) be a local hypersurface with an isolated singularity. We show that Hochster's theta pairing
) be a local hypersurface with an isolated singularity. We show that Hochster's theta pairing  . We discuss the unramified cohomology group
. We discuss the unramified cohomology group 