No CrossRef data available.
Article contents
The Coniveau Filtration on 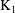 $\text{K}_{1}$ for Some Severi–Brauer Varieties
$\text{K}_{1}$ for Some Severi–Brauer Varieties
Published online by Cambridge University Press: 24 October 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We produce an isomorphism 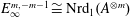 $E_{\infty }^{m,-m-1}\cong \text{Nrd}_{1}(A^{\otimes m})$ between terms of the
$E_{\infty }^{m,-m-1}\cong \text{Nrd}_{1}(A^{\otimes m})$ between terms of the 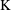 $\text{K}$-theory coniveau spectral sequence of a Severi–Brauer variety
$\text{K}$-theory coniveau spectral sequence of a Severi–Brauer variety 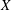 $X$ associated with a central simple algebra
$X$ associated with a central simple algebra 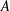 $A$ and a reduced norm group, assuming
$A$ and a reduced norm group, assuming 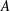 $A$ has equal index and exponent over all finite extensions of its center and that
$A$ has equal index and exponent over all finite extensions of its center and that 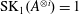 $\text{SK}_{1}(A^{\otimes i})=1$ for all
$\text{SK}_{1}(A^{\otimes i})=1$ for all 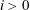 $i>0$.
$i>0$.
MSC classification
Primary:
19E08: $K$-theory of schemes
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
Artin, M.,
Brauer-Severi varieties, Brauer groups in ring theory and algebraic geometry
. (Wilrijk, 1981), Lecture Notes in Mathematics, 917, Springer, Berlin–New York, 1982, pp. 194–210.Google Scholar
Chernousov, V. and Merkurjev, A.,
Connectedness of classes of fields and zero-cycles on projective homogeneous varieties
. Compos. Math.
142(2006), no. 6, 1522–1548. https://doi.org/10.1112/S0010437X06002363.Google Scholar
de Jong, A. J.,
The period-index problem for the Brauer group of an algebraic surface
. Duke Math. J.
123(2004), no. 1, 71–94. https://doi.org/10.1215/S0012-7094-04-12313-9.Google Scholar
Gille, P. and Szamuely, T.,
Central simple algebras and Galois cohomology
. Cambridge Studies in Advanced Mathematics, 101, Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511607219.Google Scholar
Karpenko, N. A.,
Codimension 2 cycles on Severi–Brauer varieties
. K-Theory
13(1998), no. 4, 305–330. https://doi.org/10.1023/A:1007705720373.Google Scholar
Karpenko, N. A.,
Cohomology of relative cellular spaces and of isotropic flag varieties
. Algebra i Analiz
12(2000), no. 1, 3–69.Google Scholar
Karpenko, N. A.,
Chow groups of some generically twisted flag varieties
. Ann. K-Theory
2(2017), no. 2, 341–356. https://doi.org/10.2140/akt.2017.2.341.Google Scholar
Merkurjev, A. S.,
Certain K-cohomology groups of Severi–Brauer varieties
. In:
K-theory and algebraic geometry: connections with quadratic forms and division algebras (Santa Barbara, CA, 1992)
, Proc. Sympos. Pure Math., 58, American Mathematical Society, Providence, RI, 1995, pp. 319–331.Google Scholar
Merkurjev, A. S. and Suslin, A. A.,
K-cohomology of Severi–Brauer varieties and the norm residue homomorphism
. Izv. Akad. Nauk SSSR Ser. Mat.
46(1982), no. 5, 1011–1046, 1135–1136.Google Scholar
Perlis, S.,
Scalar extensions of algebras with exponent equal to index
. Bull. Amer. Math. Soc.
47(1941), 670–676. https://doi.org/10.1090/S0002-9904-1941-07536-1.Google Scholar
Peyre, E.,
Products of Severi–Brauer varieties and Galois cohomology
. In:
K-theory and algebraic geometry: connections with quadratic forms and division algebras (Santa Barbara, CA, 1992)
, Proc. Sympos. Pure Math., 58, American Mathematical Society, Providence, RI, 1995, pp. 369–401.Google Scholar
Quillen, D.,
Higher algebraic K-theory. I
. In:
Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972)
, Lecture Notes in Mathematics, 341, Springer, Berlin, 1973, pp. 85–147.Google Scholar

